Tableau Hexbins: some technical notes

I didn’t originally plan to blog a lot on technical issues even though I do a lot of analysis and datavisualization. I’m not really a hard core technical expert when it comes to tools like Tableau and there are a lot of other experts out there who record and describe interesting techniques and tools. But I’ve been working with some things recently where the existing advice isn’t very good and isn’t well explained. So I thought I’d record my experience and explanations to help me remember what I discovered and see whether the experts will pitch in to improve things. I will, however, take the opportunity to rant about the things Tableau needs to do better.

The topic is the use of hexbins in Tableau especially on maps.

Hexbins are a welcome addition to Tableau for people who want to summarise large numbers of data points in an area when plotting the individual x,y points would become confusing. They allow for the data to be summarised by the density of points in a hexagonal region. This use is well summarised by Chris Love of the Information Lab. Hexagons are nice because they are the most-sided regular polygon to tessellate the plane and this means the distortion caused by the vertices are as small as they can be (the difference between the centre-to-vertex distance and the centre-to-mid-edge distance is much lower than in a square, for example). They are the best approximation to a circle we can do in a regular tessellating polygon. And they look nice.

This is particularly cool on maps where, very often, we want to plot data which varies greatly in density. People, and data associated with people, clusters because people don’t conveniently spread out evenly but cluster together in towns and cities. And standard geographic areas (local authorities, parliamentary constituencies or super output areas^[1] etc.) tend to be based on population so have wildly differing geographic sizes depending on population density. This means that, if we plot a map based on those areas, the result will be hugely visually distorting because areas of high population density will appear very small on the resulting map even though they might be just as significant as much larger regions of very low population density. In a map of England, for example, central London looks very small but a lot of people live there; the whole county of Cumbria, where nobody seems to want to live, is huge but much less significant^[2]. So, sometimes, we want to aggregate data on maps into areas of roughly equal area. This avoids the visual distortion inherent with statistical or governmental boundaries. Hexagons look like a good candidate for quick ad-hoc areas.

So when Tableau brought in HexBin functions to group together arbitrary x,y points it looked like this would become easier. It has, but there are problems.

Lets walk through how they work and look at the issues.

The Tableau HexBin functions take x,y coordinates and bin them into hexagonal areas where the hexagons have sides of exactly one unit. On a map, Tableau plots coordinates using Longitudes (the x) and Latitudes (the y). This means that, without scaling, each hexagon has sides of length equivalent to 1 degree on the earth’s surface. But it is easy to add a scaling function to create arbitrarily sized hexagons dynamically. You just need to create a parameter for the scaling factor (in the screenshot below I’ve called it “hex density” which roughly equates to the number of hexagons per degree on a map):

This formula allows simple and easy scaling so you get the hexagon size you want that is appropriate for your map. If you set hex density to 1 (so equivalent to the default result from Tableau without scaling) on a dataset distributed across England and Wales you get this map (the points are labelled with the longitude and latitude of the centres of each heaxon):

The spacing, which looks a little odd at first sight, is a result of the geometry of a regular hexagon. For hexagons with sides of 1 unit where the top and bottom edges are oriented along lines of latitude (ie the x axis) the centre points will be 3 units apart on the x axis. The centres will be about 1.732 units apart in the y axis (go on, I dare you to work it out, it’s just basic geometry). 

This simple picture illustrates the basics of how the data is grouped. So how do we plot hexagons rather than points? This is where things get hairy. And not just stubble-hairy but more like yeti-hairy or even as hairy as one of those ridiculous Tibetan dogs^[3] sort of hairy.

Chris Love’s blog recommends plotting custom hexagon shapes on the of the points derived from the HexBin functions and a post from Kristopher Erickson goes into more detail. The biggest problem with this is that you have to manually size the custom shapes so the results tessellate and that is really annoying if you want to adjust the scaling factor and instantly see a nice map. Plus, you have to source the custom shapes. And there is another problem that the other method also suffers from which is to do with shape distortion on maps. But I’m going to postpone that until I’ve described the alternative way of drawing hexagons.

The other way is to use Tableau’s ability to plot polygons. After all, this is how we can build custom maps using areas that are not native to Tableau’s mapping services. Problem solved, or so I thought before I tried to do it.

There are not many descriptions of how to do this on the interwebs (hence this blog). But the key source for the polygon-based method seems to be from Alan Eldridge (The Last Data Bender). His key blog does a good summary of the problems that occur with custom shapes. And he proposes a solution where Tableau can generate hexagonal polygons for each hexagonal bin which will auto scale and tessellate whatever scaling factor you want to use. I’m going to walk through his method step by step, suggest some improvements and point out some of the remaining problems.

Alan’s basic idea is that we can take the coordinates of the centres of the hexagonal bins and, using simple geometry, generate the points corresponding to the vertices of the hexagon and hence plot that as a polygon. We need to generate 6 points per hexagon (obviously). If we can, somehow, generate a field for each hexagon containing the numbers from 1 to 6 we can use those as the “path” that tells Tableau what order to draw the hexagon vertices and we can use them to generate the actual x,y coordinates of each vertex using simple geometry. 

The first problem is how to get Tableau to automatically generate a field containing  the numbers from 1 to 6 for each hexbin. Alan’s method uses what is known as “Data Densification”, a somewhat obscure Tableau feature. One of the problems is that data densification is poorly documented by Tableau (the experts on it have had to reverse engineer how it works and even they admit they don’t understand it fully: Matt Lutton and Joe Mako discuss some of the ideas on this blog.) Worse, the exact Tableau behaviour seems to differ in different versions and it can be hard to reproduce at all. Alan’s demo workbook is here for those who want to test it for themselves (in my experience even reproducing the required behaviour within his workbook is hard to do). 

What his approach seems to do is to first duplicate the row-level data so that an extra field called PointID is added containing either 1 or 6 (for the duplicate rows). This involves custom SQL (which is a complication often best avoided). He generates scaled hex centre locations as described above. He then generates a unique ID for each hexbin by concatenating the strings for lat and lon locations (which by definition is guaranteed to be unique for each bin). Creating the extra numbers between 1 and 6 can then be driven by creating another field by binning PointID with a size of 1. These numbers are then used to generate a field called Angle which is used to translate the lat lon hexagon centres into vertices for each of the 6 vertices. (Actually, I’m simplifying slightly about the exact setup required to get this to work with data densification but the details are on the blog and in the workbook and they involve some serious fiddling with table calculations). In fact, I can’t even consistently reproduce the correct behaviour in copies of Alan’s workbook running in Tableau 9.1 beta.

There is a simpler way to achieve the same result that does not depend on custom SQL or data densification. It has some problems especially when data is sparse in a hexbin (with a little work these might be fixable but I wanted to describe the principles and see whether others can fix the edge cases before I get time to do it).

The trick I use is to build a custom function to generate PointID that relies on some characteristic of the underlying dataset in a way that will usually generate the numbers from 1 to 6. If there is enough numeric data in each bin and the values are well distributed then we should be able to take some integer and take the remainder mod 6. This should add an extra field to each row with the digits randomly distributed between 1 and 6 which is what we require. In the sample case below that field is called PseudoPointID and the formula for angle is:

This generates 6 angles per hexbin that enable the sheet to calculate the lat lon pairs for each hexagon vertex. The formula for this for the latitude (x coordinate) is:

And for the longitude:

Applying these calculations on a dataset^[4] for locations in england and wales generates this map (which exactly matches the hex centres in the first map above with hexagons with sides of 1 degree).

These are obviously a lot too large for useful analysis but at this point I’m just trying to illustrate the way the technique works. 

And the illustration highlights one of the major problems with Tableau’s implementation.^[5] The hexagons are squashed along the x-axis. The problem arises from spherical geometry. Travelling a degree west from the centre of London takes you about 37km but travelling a degree north takes you 111km on the spherical surface of the earth. Visually the map doesn’t look that distorted because the effect is partially compensated for by the distortions inherent in the Mercator projection which stretches horizontal distances depending on latitude. But the compensation isn’t exact and the visual result varies by latitude. At least the distorted hexagons tessellate. It is beyond my brain’s ability to worry about whether the distance distortion is significant for analytic purposes but grappling with this is for another day. Besides, with a bit more spherical geometry we could compensate for this by applying different (latitude-dependent) scaling factors for the coordinates. But that, too, is for another day.

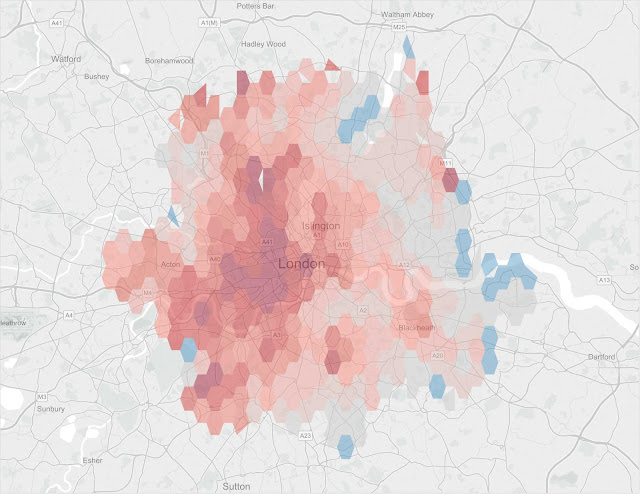
There is another issue with this approach which is that it is hard to guarantee that each hexagon has enough underlying points to create a complete hexagon when the data is sparse. What this looks like on a map is shown below. (Update. If you actually examine the problematic hexagons, you find that some do have enough points but for some reason they don't plot. It is true that points with smaller numbers of original lat/lons tens to be the ones that don't plot but the actual reason why they don't plot is a bit of a mystery).

The underlying data being plotted is 2014 house prices versus the national average where the town is recorded as “London”.^[6] Hexes near the edge of the area have fewer than a handful of transactions (and therefore even fewer locations as each postcode may cover more than one house). They therefore don’t always have enough PointIDs to generate enough points to create the vertices for a complete hexagon.

But we can generate maps that work over a very wide range of scales. The map above has a hexdensity of 50 and the one below has a density of 100.

So we have something that (mostly) works. It is easier to understand how to do it than techniques involving data densification. And it always works (unlike data densification which is hard to understand, hard to control and flakier than a well-made french croissant). We can generate maps with (approximately) equal area hexagonal tessellting bins. We can scale them over a very wide range and they still work with very few mapping artefacts. 

Now for the complainy bit. Tableau could have made this much easier: Tableau could build in parameters to control the scaling; they could auto-generate the polygons or their vertex coordinates; they could build in the maths to do the scale adjustments to make maps on Mercator projections work properly (though they might need to allow for some user choices about how that would work). I do hope that, as people start exploiting HexBins, Tableau will enhance their utility by adding this functionality.

PS My experimental workbook for the above examples is too big for Tableau Public so I can't link to it here. But I have a workbook that just uses the postcode locations (of which there are about 2.5m) that illustrates the way hex bins work. It is a little dull as the density of postcodes is basically an unreliable proxy for population density. But the workbook is here for those who want to check out the formulae or some simple analysis of how UK postcodes work.

---

[1] Super output areas were designed to create geographic areas for statistical analysis based on population (in England and Wales; Scotland and N Ireland decided to be awkwardly different but actually have similar units). Lower-layer super output areas (LSOAs) are designed to contain about 1,500 people each and are widely used for small area census and health statistical analysis. 

[2] About 20 times more people live in greater London in about ¼ of the area.

[3] The Lhasa Apso, for example, seems to have more hair than dog.

[4] The underlying dataset is house price transactions in england and wales. For each year there are nearly 1m identified transactions where we know the price and the property postcode and therefore location.

[5] Another is that there are bugs in Tableau 9.1 in the HexBin implementation in Goggle’s BigQuery connector which is my favourite analytics engine for BigData stuff. I’ve reported them to tableau in the beta. The results here are all done from extracts.

[6] There is a lot more to be done with this dataset. In case you wonder, the colour scale is set so that below-average prices are blue and above-average prices are red. The very dark red hexes in central London are areas where average prices paid in 2014 were more than 4 times higher than the national average.

Don’t start sanctioning GPs until they have access to all the data

We should not start sanctioning GPs for their antibiotic prescribing until all the data is widely available so they and their managers can benchmark their behaviour against everyone else.

The situation
There is a disturbing amount of variation in the number of antibiotic prescriptions issues by GPs in England. About 60 practices (out of a little under 8,000) prescribe at a rate more than ten time higher than the national average and more than 300 at a rate of more than double the national average. at the other end of the scale about 200 prescribe at less than half the national average rate. (all these numbers are based on the calendar year 2014 when more than 35 million prescriptions were issued).
Even if we average across whole CCGs there is a lot of variation. Here is a map of the relative amount of prescribing at CCG level (all numbers are normalised for the population mix of the people on GP lists, taking account of the distribution of different age groups).

The average number of prescriptions in the top CCG is twice the national rate and the lowest prescribing CCG prescribes just two thirds of the national number.

We can see that the GP variation is much wider in the next plot. In this chart each blue dot is an individual GP practice and all are shown relative to the population-normalised national average number of prescriptions. The red marks are box-plots, a statistical way of summarising the amount of variation in each (old style) NHS area team. The two-colour red blocks show the median (the middle line) and cover 50% of all the GP practices within each area. The plot excludes the 80 most extreme GP practices.

we can drill into this data to see some further detail for a region. The chart below shows every GP in london grouped by CCG.

Of course, some of the most extreme outliers here might be anomalies caused by GP practice closures or openings mid year (I don’t have the local knowledge to fix this without a lot of work). But the point stands: there is a lot of variation and no good reason to explain it other than GP behaviour.
We can even drill further into the data to look at the mix of antibiotic types used by each practice. This map shows the mix and relative amount of prescribing in Bradford and Bradford Districts CCGs (the city and the surrounding area). The size of each pie is the relative number of prescriptions with the volume of each class of drugs as the size of each slice. Not that the GPs in the city seem to issue far more prescriptions than the GPs in the surrounding area. The mix is also a little different.

So What?
I show these analyses not to heap criticism on GPs but to show the sort of analysis that should be used to help analyse and challenge the variation.

The NHS doesn’t have accessible analysis that does this job.

What is accessible and free is a clunky, awkward and obsolete system called ePact provided by the NHS BSA. This system is free to GPs and Medicine Managers (the people whose job it is to challenge GP prescribing behaviour). It manages to be bad value for money despite being free by requiring vast amounts of time and effort to use despite not making access to all the relevant national data easy.

My analysis is based on the publicly available monthly data downloaded from the HSCIC website (it’s a lot of data with nearly 600 million rows of GP-level data so far summarising about 5 billion prescriptions). I store it in Google’s BigQuery tool and analyse it using Tableau. This makes analysing the entire dataset (with monthly data from 2010) interactive even if you want to see what a single GP practices does with a single formulation of an individual drug.
Until the NHS has started to make this sort of analysis accessible to all GPs and medicine managers it is counterproductive and damaging to sanction the GPs for their behaviour. We know that, when benchmarking data like this is made accessible, the unwanted behaviours will change (or some of them will).

The first step in changing unwanted habits is showing the data. we should not be complaining about it until that basic step has happened.

Government needs to develop better ways to make spending decisions

Government's’ failure to understand return on investment is catastrophic when budgets are being cut

The recent announcement of a new rounds of cuts to public health budgets (see the Kings Fund analysis here) has highlighted something rotten in the way government makes spending decisions. It smacks to me of something I’ve suspected for a long time: governments don’t have a sensible, logical or reasonable way to make good decisions about where and how their money is allocated.

The issue isn't as simple as “evil tory cuts” (though that is how many headlines will portray it) because Labour governments have also shown the same underlying failure to understand the difference between good and bad ways to spend their (or, as some would say: your) money.

The difference between Labour and Conservative ideas is often portrayed to be between those who want to spend more and those who want to spend less. Though both flavours of politician in the UK have run the country at times of both austerity and plenty and both have presided over regimens where both more spending and less spending have been appropriate. Both, however, have failed to show much insight into how to make the decisions about where the money ought to go.

There are several parts that contribute to this failure. One is that most government decisions are made top-down; they worry about the totals but not the details. Another is that many decisions are essentially political: that is they are determined by what looks good rather than what actually works. Inertia plays a role: once started many government activities are hard to stop and radical shifts in the allocation of money are hard to make. Fragmentation of decision making plays another role: the impact of decisions in one department on the costs in another are rarely considered carefully. Overall the impact of spending is rarely a serious part of decisions about the amount of spending (let’s call this a failure to understand Return on Investment (ROI) even though I’m broadening the terminology beyond its normal use in business).

In simple language there is certain tendency in governments spending more to believe that the only thing that matters is that more is spent. And those governments pursuing cuts tend to focus on the headline departmental budgets with little consideration for the long term effect on either outcomes or even the impact on total government spending in future years.

Businesses don’t do decision making like this. Or, to be more precise, those businesses who do make bad decisions persistently get driven to bankruptcy by the competitors who make better decisions. Governments lack this corrective mechanism and can persist with utterly rotten decisions on a scale impossible in even the largest private enterprise. In fact, while private sector firms are ultimately disciplined by competition and have to correct bad decisions or fail, governments have a built in tendency to never admit their failings--that looks bad in headlines--and therefore persist with bad ideas for much longer and on a larger scale.

The point I want to make is that good decision making in many businesses has characteristics that are frequently absent in government. In particular, successful businesses are good at considering the effect on the whole business of each spending decision. And, they tend to be smart at recognising when more spending in one area will lead to lower cost or greater success in another.

The core problem is that not all spending is equal; not all projects deliver the same results; not all budgets have an equal impact on their desire outcomes. Effective decision makers know this and direct their money towards the places where the biggest bangs per buck are achieved (or the return on investment is highest). This principle applies whether the money available to spend is plenteous or tightly constrained.

Another, more subtle point, is that the relationship between what you get and how much you spend is far from linear. Sometimes there is a minimal amount that must be spent to achieve anything; sometimes spending twice as much gets you little more than spending the right amount; sometimes a small spend in one area releases the possibility of a large benefit somewhere else.

Take the world of supermarkets. They succeed when the put the right goods on their shelves, at the right time, at the right prices to please their customers and do all this without spending an excessive amount on the logistics of the process. Supermarkets do this well not (just?) by screwing their suppliers on price but by having excellent logistics processes (which, in practice, means a lot of spending on tightly integrated IT systems to coordinate the whole supply chain from production, through delivery to shelf-stocking.) They are well aware that to succeed with customers means spending a great deal of money on things that don’t obviously have anything to do with customers (like IT and logistics).

In contrast, governments are often oblivious to the need to spend here to achieve a benefit there. They tend to impose blanket cuts across all departments when they need to cut back rather than asking whether increased investment in some areas could yield savings somewhere else. Hence cuts in public health spending when the NHS is faced with growing amounts of illness. Or cuts to the ONS when the government is already seriously lacking in good quality information about what is happening in the country (in fact, how does government work out whether any policy is working when its information about outcomes is poor to start with and the budget to collect better information is being cut further?)

The NHS is a microcosm of government kakistocracy here. To know whether the treatments offered by hospitals and GPs are any good we need vast quantities of high quality information about activity and outcomes. We get very little of either as NHS spending on data collection and analysis is a shockingly low outlier in the world of large organisations (headlines are made by declaring that a larger share of the money will go to “frontline care” when we are not prepared to spend the basic minimum to ensure that we know whether that frontline care is doing good or causing harm). Worse, the really big opportunities to improve the NHS are not in major top-down changes to the organisation or public behaviour but in the steady accumulation of small good ideas about how to do things better at the front line. But the only way to achieve cumulative improvement is to monitor activity and outcomes carefully (which means spending on data collection and IT) and to use this information to drive behaviour towards the things that work best. If we really wanted to save money in the NHS (and/or improve the outcomes) we would invest more in data and analysis with the benefit that medical practice would improve over time both saving money and leading to better results. Neither the naive belief that just spending more will make things better nor the opposite belief that cuts should come from somewhere other than the front line actually help much at all (we’ve tried both in the last decade).

Only a careful analysis of which spending will yield system-wide benefits will give a good return on investment in the NHS. So cutting public health budgets is easy to do but may cost more for the NHS as a whole in the future (probably: there may well be many public health projects that have little effect on outcomes or NHS costs but it is fairly clear that the recently announced cuts were not based on any such analysis). adding more staff to the NHS improves capacity but lowers productivity making it a worse investment than spending more to automate the tedious data collection that is often paper-based and wastes vast amounts of medical time.

The general point for government is that thinking about ROI is essential both when budgets are tight and when they are generous. Spending money on the wrong things yields far less benefit that it should; cutting the wrong projects yields far lower savings for government as a whole than it should. Discriminating far more carefully when spending decisions are being made (both when cutting and expanding the budget) could give major gains in how well public services work. Yet there is little evidence that this thinking is part of the way decisions are made on public spending.